PHOTOMÉTRIE

PHOTOMÉTRIE

La photométrie proprement dite s’occupe de la comparaison quantitative des lumières (émises par des sources, transportées par des faisceaux ou agissant sur des récepteurs), d’après leur perception par l’œil. Elle est dite objectivement homochrome si les lumières étudiées ont toutes la même couleur, leurs compositions spectrales étant en outre identiques ou très voisines. Si ces compositions spectrales diffèrent notablement, les couleurs pouvant avoir cependant même apparence (lumières subjectivement homochromes), et a fortiori si les couleurs ne sont pas les mêmes (lumières hétérochromes ), des conventions doivent intervenir, fondées sur les réponses d’un observateur moyen , notion sur laquelle on reviendra.

La photométrie physique utilise des récepteurs autres que l’œil, étalonnés de façon que le résultat des mesures soit le même qu’en photométrie visuelle. Mais on donne aussi, par extension, le nom de photométrie (plus souvent que celui de radiométrie ) à la mesure des flux d’énergie transportés par les rayonnements, qu’ils soient visibles, infrarouges ou ultraviolets, et des grandeurs qui s’y rattachent. La spectrophotométrie évalue les divers constituants monochromatiques d’une lumière complexe, ou compare, longueur d’onde par longueur d’onde, des lumières diverses.

Les grandeurs que l’on devra considérer ici (éclairements, flux, intensités, luminances, etc.) et les unités correspondantes (lux, lumen, candela, nit) sont reliées par des définitions qui se transposent aisément du cas des appréciations visuelles à celui des déterminations énergétiques.

Depuis les premiers traités publiés au XVIII^e siècle par P. Bouguer et par J. H. Lambert (1729 et 1760), le langage de la photométrie s’est progressivement précisé, grâce en particulier aux travaux d’André Blondel et de la Commission internationale de l’éclairage (C.I.E.). Sa connaissance et celle des étalons et des techniques mises en œuvre sont indispensables pour l’étude de nombreuses applications concernant l’éclairagisme, l’optique physiologique, l’action biologique ou chimique des radiations, ainsi que l’optique instrumentale et les conditions d’émission ou d’absorption des rayonnements par la matière.

1. Grandeurs et unités intervenant en photométrie visuelle

Les définitions de grandeurs et unités intervenant dans cet article sont conformes aux recommandations de la C.I.E. On traitera d’abord de la photométrie visuelle homochrome.

Éclairement et flux lumineux

On dit que deux surfaces ont le même éclairement si, lorsqu’on les recouvre d’écrans diffusants blancs, ces derniers présentent le même aspect dans des conditions identiques d’observation (plages juxtaposées, par exemple). Soit une surface éclairée, d’abord par une source ¹, puis par une source ², enfin par ¹ et ² simultanément, les sources ne se masquant pas l’une l’autre, les éclairements correspondants E¹, E² et E sont, par convention, tels que:

Le tableau 1 donne quelques exemples d’éclairement. Ces grandeurs sont mesurables; dans le système international, l’unité d’éclairement est le lux (symbole lx) défini ci-après; on emploie aussi le phot (ph) valant 10⁴ lux.

Le flux lumineux F reçu par une surface d’aire S est, par définition, le produit de S par son éclairement E. Si celui-ci n’est pas uniforme, F prend la forme d’une intégrale d’espace étendue à la surface considérée:

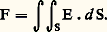La règle d’additivité des éclairements entraîne celle des flux lumineux. L’unité correspondante, le lumen (lm), est le flux reçu par une surface de 1 m² dont l’éclairement est partout 1 lux.

Le flux lumineux F est, pour une lumière de composition spectrale déterminée, proportionnel à la puissance transportée, dite flux d’énergie 淋, évaluée en watts. L’efficacité lumineuse du rayonnement considéré, nulle pour les lumières invisibles, est égale au rapport K du flux lumineux au flux d’énergie, soit:

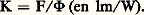Dans un milieu non absorbant, quel que soit l’endroit où on le mesure, le flux 淋 d’un faisceau est constant. De même, F est indépendant de la surface sur laquelle on le détermine, et la somme des flux de tous les faisceaux émis par une source est égale au flux lumineux de cette source.

L’émittance d’une source en un point O est le rapport M = d F/d , d F étant le flux lumineux émis dans toutes les directions par l’élément de surface d entourant O (fig. 1). M s’exprime en lumens par mètre carré. L’émittance d’une surface qui n’est ni lumineuse par elle-même ni luminescente est, au plus, égale à son éclairement.

Source ponctuelle et intensité lumineuse

Une source est dite ponctuelle si sa dimension transversale la plus grande est très petite par rapport à la distance qui la sépare du système d’utilisation (écran récepteur, etc.). Un rapport dimension-distance égal à 1/100 permet, dans la plupart des cas, une précision de mesure convenable.

L’intensité lumineuse I d’une telle source ponctuelle, dans une direction (fig. 2), est par définition égale au quotient du flux élémentaire d F, émis par la source à l’intérieur d’un cône infiniment petit de sommet O contenant , par l’angle solide d 行 de ce cône:

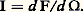Rappelons que cet angle solide a pour mesure (en stéradians) le quotient par x ² de l’aire découpée par le cône sur une sphère de centre O et de rayon x . Si le cône s’appuie sur un élément d’aire d S entourant un point A et tel que la normale AN à cet élément fasse avec un angle , on a:

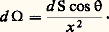L’éclairement en A est par suite:

L’unité d’intensité lumineuse est la candela (symbole cd), antérieurement appelée bougie ; elle vaut un lumen par stéradian. Elle est en réalité définie à l’aide d’un étalon que l’on décrira plus loin, et les unités de flux (lumen) et d’éclairement (lux) en dérivent.

Luminance

La luminance L (antérieurement appelée éclat , puis brillance ), dans une direction , d’un élément de source de faible surface entourant un point O (fig. 3) est, par définition, égale au rapport: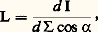

d I étant l’intensité de l’élément dans la direction , d sa surface et 見 l’angle formé par et la normale OK à l’élément. L’unité de luminance le plus souvent utilisée est la candela par mètre carré, appelée aussi nit (nt). Le stilb (sb) est égal à une candela par centimètre carré (1 sb = 10⁴ nt). Le stilb vaut 3,14 憐 10⁴ blondels , cette dernière unité étant parfois employée en éclairagisme. Le tableau 2 indique quelques valeurs de luminances. Une luminance dépassant plusieurs centaines de milliers de nits peut être dangereuse pour l’œil, d’où l’emploi fréquent de réflecteurs et de diffuseurs convenables.

L’éclairement d E que la source élémentaire d’aire d et de luminance L produit sur une surface, disposée comme l’indique la figure 3, s’exprime donc par:

d 切 étant l’angle solide sous lequel l’élément d est vu du point éclairé A. On peut, à l’aide de la formule précédente, calculer l’éclairement dû à des faisceaux provenant de sources dont la luminance est connue dans chaque direction, sans qu’interviennent ni la distance, ni la surface, ni l’orientation de ces sources. C’est le cas, par exemple, de l’éclairement produit par le ciel à travers une fenêtre.

Quand la luminance L d’une source est la même dans toutes les directions d’émission, la source est dite orthotrope ; on dit encore qu’elle obéit à la condition de Lambert. On peut montrer qu’alors son émittance est M (lm/m²) = 神 L (cd/m²). Si, par exemple, une feuille de papier blanc placée au soleil (E 力 100 000 lx) n’absorbe qu’une fraction négligeable de la lumière, son émittance est proche de 100 000 lm/m² et sa luminance est de 100 000/ 神 力 30 000 nits.

Facteurs de réflexion, de transmission et d’absorption

Si, à propos d’une surface, Fⁱ , F^r , F^a , F^t sont, respectivement, les flux incident, réfléchi, absorbé et transmis, on définit les trois facteurs suivants:

– facteur de réflexion: 福 = F^r /Fⁱ ;

– facteur de transmission: 精 = F^t /Fⁱ ;

– facteur d’absorption: 見 = F^a /Fⁱ .

Si l’on tient compte, dans l’évaluation de 福, de toute la lumière réfléchie, on a: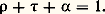

Ces trois facteurs dépendent, dans certains cas, de la composition spectrale de la lumière. Les facteurs de réflexion et de transmission des surfaces vitreuses varient avec les indices des milieux qu’elles séparent, selon des lois établies par Fresnel (cf. LUMIÈRE - Réflexion et réfraction). En lumière monochromatique (et, en lumière complexe, pour les corps «gris», dont l’absorption ne varie pas avec la longueur d’onde), dans un milieu homogène qui n’est pas parfaitement transparent, le flux transmis décroît de manière exponentielle en fonction de l’épaisseur (cf. DIFFUSION DE LA LUMIÈRE - Météorologie).

Il est souvent commode de considérer la densité optique d’une lame absorbante: cette quantité est définie comme le logarithme de l’inverse de son facteur de transmission: D = Log 1/ 精. Lorsqu’on superpose deux lames non colorées, leurs densités optiques s’ajoutent si les pertes de lumière par réflexion sont négligeables devant les pertes par absorption.

2. Techniques de la photométrie visuelle

Méthodes de gradation de la lumière

On ne peut effectuer avec précision des mesures photométriques visuelles, même homochromes (le cas des mesures hétérochromes est examiné dans le chapitre suivant), que lorsqu’elles portent sur la comparaison de deux luminances «vues» simultanément. Et même dans ce cas, alors que l’égalité de deux luminances peut être sensiblement appréciée, il est impossible d’évaluer quantitativement le rapport entre deux luminances différentes. On est par suite amené à utiliser deux plages photométriques constituées par deux écrans identiques généralement juxtaposés, éclairés et observés sous des angles égaux pour que les luminances soient directement reliées aux éclairements. Lorsqu’elles sont égales, on dit qu’il y a «équilibre photométrique». Si deux éclairements sont à comparer, il faut pouvoir rendre l’un d’entre eux égal au second, en le réduisant (ou en l’augmentant) dans un rapport connu. On dispose, à cet effet, de modes de gradation de la lumière dont on va indiquer les plus usuels.

Le procédé le plus simple consiste à agir sur la distance x séparant la plage considérée de la source lumineuse: dans ce cas, E est inversement proportionnel au carré de la distance si l’angle d’incidence des rayons est constant. Mais cette méthode n’est valable que si la valeur de x est environ cent fois plus grande que le diamètre de la source (source ponctuelle). Cette condition nécessite souvent des dispositifs encombrants, d’où l’emploi fréquent d’autres modes de gradation qui sont, au besoin, étalonnés par comparaison avec cette «loi des distances».

À l’aide d’un diaphragme, on peut jouer sur la surface d’une source ayant une même luminance en tous ses points (ou sur sa longueur, si elle est filiforme). Cette méthode simple et pratique est malheureusement peu précise.

On peut encore placer, comme l’indique la figure 4, sur le trajet des rayons dont on veut réduire l’effet lumineux, un disque de Talbot, à secteurs alternativement opaques et évidés; on le met en rotation à une vitesse suffisante pour utiliser la persistance des impressions lumineuses. L’expérience montre que l’éclairement de la plage photométrique, qui paraît alors constant, est réduit dans le rapport 見/2 神, 見 (radians) étant l’angle au centre total des secteurs évidés.

On utilise parfois la loi de Malus (cf. LUMIÈRE - Polarisation), d’après laquelle le flux lumineux varie comme le carré du cosinus de l’angle que font entre elles les directions des vibrations transmises par un polariseur et un analyseur placés l’un derrière l’autre sur le trajet des rayons. Mais il est essentiel, si c’est le polariseur que l’on fait tourner pour effectuer le réglage, d’utiliser une lumière qui n’a pas été polarisée auparavant; si l’on agit sur l’analyseur, il faut que la lumière ne puisse pas, après l’avoir traversé, être transmise ou réfléchie par d’autres corps d’une façon variable selon sa polarisation.

On peut aussi réduire un flux lumineux par interposition d’un filtre absorbant, formé soit d’une lame à faces parallèles, soit d’une association de deux coins d’angle aigu (fig. 5), mobiles l’un par rapport à l’autre de façon que l’on puisse régler l’épaisseur traversée. La transmission obtenue dépend, en général, de la longueur d’onde, même si ces filtres sont dits neutres (non sélectifs); aussi doivent-ils être étalonnés pour les lumières auxquelles on les destine.

En recommençant plusieurs fois une mesure photométrique, on constate une certaine dispersion des résultats. Dans les cas les plus favorables (déterminations homochromes, moyenne de cinq valeurs au moins trouvées par un observateur exercé), l’incertitude relative ne tombe pas au-dessous de quelques millièmes; elle est souvent très supérieure.

Réalisation des plages

On constate que l’incertitude des mesures est d’autant plus réduite que les plages photométriques sur lesquelles sont reçues les lumières à comparer sont plus étroitement juxtaposées. Dans le dispositif de Ritchie, par exemple, ces plages sont les faces P et P d’un prisme de plâtre à arête très fine A, éclairées et observées comme l’indique la figure 6.

Le cube de Lummer et Brodhun, d’emploi fréquent, est formé de deux prismes transparents rectangles isocèles (fig. 7), accolés par leurs faces hypoténuses, dont une région P assure, comme à travers une lame à faces parallèles, la transmission d’une des lumières (c’est l’une des plages), alors qu’il y a réflexion sur la région P du premier prisme, qui est métallisée ou bien séparée de l’autre prisme par une mince couche d’air. Des lames blanches L et L , diffusant par transmission (parfois par réflexion) la lumière des sources S et S à comparer, sont observées à travers cet ensemble. P et P sont rectangulaires, ou constitués par deux demi-cercles juxtaposés, ou sont formés par un petit cercle entouré d’un anneau. La ligne qui les sépare peut être rendue extrêmement fine, et disparaître au moment où leurs luminances sont égales.

Dans le photomètre de Bunsen (fig. 8), un écran translucide, qui peut être en papier blanc, comporte une région centrale P¹ (une tache d’huile, par exemple), dont les facteurs de transmission et de réflexion sont différents de ceux du pourtour P². Les lumières étudiées sont dirigées perpendiculairement à cet écran. Les deux faces sont observées à l’aide de miroirs M et M , l’œil Œ étant placé dans le plan de symétrie de l’appareil. L’équilibre correspond à la fois à une égale luminance des images de P¹ et de P² et à un égal contraste de chaque image de P¹ par rapport à celle de P² qui l’entoure.

Citons également les cubes de Lummer à contrastes, combinant les avantages du dispositif précédent et ceux d’une très bonne juxtaposition des plages à confronter.

Mesure des intensités

On utilise un banc photométrique (fig. 9) pour comparer deux intensités lumineuses I et I provenant de deux sources S et S .

Cet appareil est constitué de deux rails parallèles sur lesquels peuvent se mouvoir, sur quelques mètres, les sources à étudier et/ou la «tête» portant les plages photométriques. Dans le cas du schéma, l’œil Œ observe, à travers un cube de Lummer K, les deux faces P et P d’un écran diffusant, par réflexion sur deux miroirs M et M . On fait varier les distances x et x séparant S et S de l’écran, ou l’une d’entre elles; quand les luminances paraissent égales, on a I /I = x ²/x ². Si I est très supérieur à I, on interpose entre S et P un disque de Talbot ou une lame absorbante de transmission connue.

Pour l’étude de sources de lumière peu intenses, on se sert parfois de photomètres sans écran diffusant , les sources S et S étant placées respectivement aux foyers objets de deux lentilles L et L (fig. 10) de longueurs focales f et f ; l’œil Œ se trouvant au foyer image de l’oculaire Oc regarde la face hypoténuse du cube K. Pourvu que les images de S et S soient superposées et à l’intérieur de la pupille, on a I /I = f ²/f ² lorsque l’équilibre photométrique est atteint, ce qui ne peut se faire que par une des méthodes de gradation sans variation de distance.

Lorsqu’on a besoin de connaître les intensités I d’une source S dans toutes les directions de l’espace, et qu’il est impossible d’orienter S d’une manière quelconque, on utilise des systèmes de miroirs à incidence constante. Celui de la figure 11 est constitué de deux miroirs M¹ et M² pouvant tourner ensemble autour de l’axe XX sur lequel sont placées la source S, une source tare T et la tête photométrique Ph. L’ensemble M¹-M² permet d’étudier la répartition de I dans un plan normal à l’axe XX .

Étalons photométriques

L’étalon primaire, qui sert à définir l’unité d’intensité lumineuse, fut constitué à l’origine par des bougies, puis par des lampes à flamme, telles que la lampe à huile de Carcel, puis par des lampes électriques à incandescence; c’est aujourd’hui un «corps noir» (enceinte à température uniforme, percée d’une très petite ouverture). La recherche d’une précision accrue a ainsi conduit à la définition actuelle de la candela (nom donné à l’ancienne bougie, dans un but d’unification internationale): c’est la soixantième partie de l’intensité, en direction normale, d’un centimètre carré de corps noir à la température de solidification du platine (1 773 ⁰C). Cette température est reproductible, car le platine reste pur si on le chauffe par induction à haute fréquence dans un creuset de thorine (ThO²).

Les étalons secondaires usuels, calibrés par comparaison directe ou indirecte avec l’étalon primaire, sont des lampes dont le filament de carbone ou de tungstène est situé dans le vide; la couleur des premières est voisine de celle du corps noir (platine), les secondes se rapprochant davantage de nos sources d’éclairage habituelles. Le filament de ces lampes est disposé dans un plan: on oriente celui-ci normalement à la direction d’utilisation.

Ces lampes sont «formées» après quelques dizaines d’heures de fonctionnement. Si on règle la tension d’alimentation à quelques dix-millièmes près, l’intensité lumineuse est stable à quelques millièmes près. Au bout d’une centaine d’heures d’utilisation, la volatilisation du carbone ou du tungstène qui se dépose sur la paroi rend celle-ci plus absorbante, et, la résistance électrique augmentant, la lampe devient inutilisable pour des mesures précises.

Bien souvent, l’une des plages photométriques est éclairée par une source tare (dont l’intensité peut n’être pas connue, mais doit être maintenue constante), l’autre plage étant éclairée successivement par les deux sources à comparer. Cette méthode, qui rappelle celle des pesées à tare constante, a l’avantage d’éliminer certaines causes d’erreur tenant au manque de symétrie des dispositifs de mesure.

La tare est presque toujours une lampe à filament, dont la forme peut différer de celle des étalons secondaires et dont les conditions d’emploi, analogues à celles de ces derniers, sont plus ou moins rigoureuses selon le degré de précision désiré.

Mesure des flux et des éclairements

Il est parfois utile de connaître le flux total F d’une source plutôt que son intensité I dans telle ou telle direction. On utilise, pour calibrer des étalons secondaires de flux, la relation:

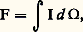(l’intégrale étant étendue à tout l’espace) ou plutôt une somme remplaçant cette intégrale.

Quant à la comparaison directe de deux flux, elle peut se faire à l’aide d’un lumen-mètre tel que celui d’Ulbricht-Blondel. C’est une sphère creuse opaque (fig. 12), garnie intérieurement d’un enduit diffusant blanc très peu absorbant, et comportant une petite fenêtre p munie d’un verre dépoli. L’une ou l’autre des sources à comparer (soit S, de flux F) est placée à l’intérieur de (au voisinage du centre) et un écran opaque blanc E empêche S d’éclairer directement p . On peut montrer que l’intensité lumineuse de cette fenêtre, mesurable à l’aide du photomètre Ph, est sensiblement proportionnelle à F, à condition que les dimensions de p , de S et de E soient petites vis-à-vis du rayon de .

Pour la mesure des éclairements, on utilise des luxmètres , les luminancemètres (ou nitomètres ) servant à celle des luminances. Le principe de ces deux types d’appareils est le même. En effet, la mesure de l’éclairement en un point se ramène à celle de la luminance d’un écran blanc diffusant (plaque d’essai), placé en ce point dans le plan à étudier. La lampe tare dont sont munis ces instruments est alimentée par un dispositif de contrôle du courant qui la traverse. Ces appareils, souvent gradués en lux ou en nits, sont calibrés soit à l’aide d’un étalon de luminance, soit en envoyant sur la plaque d’essai un éclairement connu. Bien que, dans la plupart des applications, une marge d’incertitude de quelques centièmes soit tolérée, il faut signaler les principales sources d’erreurs possibles, telles que instabilité de la lampe tare, jeu des pièces mécaniques, lumières et ombres parasites.

3. Photométrie hétérochrome

On ne saurait limiter les mesures photométriques au cas des lumières ayant la même couleur que l’étalon primaire d’intensité lumineuse. Des comparaisons hétérochromes s’imposent, non seulement parce que les diverses lumières dites blanches ne sont pas, en fait, rigoureusement homochromes, mais encore parce qu’on utilise de plus en plus fréquemment des lampes au sodium, au mercure ou au néon qui produisent des lumières très colorées. On notera, en outre, l’intérêt des physiciens et des physiologistes à l’égard des mesures de l’efficacité lumineuse des divers rayonnements visibles. La difficulté des comparaisons hétérochromes a conduit à faire appel à des méthodes et à des conventions qui vont être indiquées.

L’examen de plages juxtaposées , comme dans les mesures homochromes, convient à l’étude de lumières de couleurs peu différentes. Dans l’appréciation des luminances, on doit faire abstraction des écarts de couleurs, lesquels contribuent, pour une large part, à la dispersion des résultats obtenus par un même observateur, ainsi qu’à la divergence des résultats moyens provenant d’observateurs différents. L’étendue du champ visuel joue dans ce cas un rôle prépondérant. Les flux lumineux ainsi mesurés ne sont plus proportionnels aux flux d’énergie, quand ces quantités deviennent très faibles ^{[cf. VISION]}.

La méthode de cascade consiste, quand on veut comparer les intensités I et I de deux sources S et S , à utiliser des sources auxiliaires S¹, S²..., Sⁿ ayant des couleurs régulièrement réparties entre celles de S et S et des intensités I¹, I²..., Iⁿ . On évalue les rapports I¹/I, I²/I¹..., I /Iⁿ , d’où l’on tire le rapport I /I cherché:

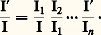L’évaluation directe de I /I serait moins précise que chacune des mesures intermédiaires, rendue faiblement hétérochrome. Toutefois, les n + 1 mesures qui sont nécessaires risquent, par accumulation d’erreurs, de rendre le résultat assez incertain.

Dans la méthode de papillotement , on substitue l’un à l’autre, sur la même plage photométrique, à intervalles réguliers, les deux éclairements E et E à comparer. La rotation autour de l’axe A du disque D à demi évidé (fig. 13) fait que l’œil Œ reçoit alternativement les lumières des sources S et S , respectivement réfléchies par les miroirs M et M . Au-delà d’une certaine valeur de la fréquence f de substitution des deux lumières, la fluctuation de celles-ci n’est plus perçue. Au-dessous d’une fréquence plus ou moins inférieure à la précédente, les variations de couleur reparaissent. Entre ces deux limites, on peut faire disparaître l’effet de papillotement en réglant convenablement l’un au moins des éclairements. On admet qu’alors E et E sont égaux. Cette méthode, actuellement peu employée, permet, dans des conditions convenables, d’obtenir des résultats comparables à ceux des précédentes.

Quel que soit le choix de la méthode, on ne doit pas espérer, en photométrie hétérochrome, réduire l’incertitude à moins de quelques centièmes (au mieux). Les laboratoires spécialisés, qu’il est préférable de consulter pour procéder à des mesures de qualité, utilisent des étalons secondaires ayant les couleurs des lumières à étudier et des filtres colorés dont on connaît les coefficients de transmission globale pour les lumières les plus courantes.

4. Mesure énergétique des rayonnements

Grandeurs énergétiques

À la puissance, dite aussi flux d’énergie , 淋 (watts), transportée par un faisceau de radiations, on fait correspondre des «grandeurs énergétiques» rattachées à 淋 comme les grandeurs photométriques le sont au flux lumineux F. Les formules ci-après suffiront à les définir.

Soit d 淋 le flux d’énergie reçu par une surface d’aire d S, ou bien émis par une surface d , ou encore émis dans un angle solide d 行 (fig. 1, 2, 3), l’éclairement énergétique , l’émittance énergétique (exprimées en W/m²), l’intensité énergétique (exprimée en W/std) seront respectivement:

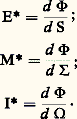Soit d I, d’autre part, l’intensité énergétique d’un élément d’aire d , dans une direction faisant l’angle 見 avec la normale à cet élément, sa luminance énergétique (exprimée en W/m²) est:

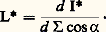Nous avons affecté des astérisques aux symboles des grandeurs ci-dessus pour les distinguer des symboles des grandeurs photométriques correspondantes.

Il résulte de ces définitions que les relations établies en photométrie visuelle se transposent au cas de la photométrie énergétique. x étant la distance de la source ponctuelle à la surface éclairée, l’angle de la normale à cette surface avec la direction des rayons incidents, d I l’intensité lumineuse de l’élément d , 見 l’angle de la normale à l’élément avec la direction des rayons et d 切 l’angle solide sous lequel d’un point de d on voit d S, on a:

et, pour une source satisfaisant à la condition de Lambert, on a: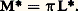

Pour une lumière de composition spectrale déterminée, la relation définissant l’efficacité lumineuse K se généralise comme suit:

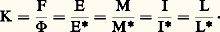Soit un faisceau de flux d’énergie 淋 et de flux lumineux F, transportant, entre les longueurs d’onde et + d, des flux d 淋 et d F. Les quotients 淋 size=1^凞 = d 淋/d et F size=1^凞 = d F/d sont appelés respectivement flux énergétique et flux lumineux par unité de longueur d’onde, pour la longueur d’onde; on dit souvent, en abrégé, flux monochromatique ou encore flux spectral , le symbole utilisé permettant d’éviter toute confusion: d 淋 et d F s’évaluent en fractions de watt et de lumen, et d en fractions de mètre, généralement en nanomètres (10 size=1^漣9 m).

On définit, d’une façon analogue, les éclairements E size=1^凞 et E size=1^凞 monochromatiques ou spectraux, les émittances M size=1^凞 et M size=1^凞, les intensités I size=1^凞 et I size=1^凞 et les luminances L size=1^凞 et L size=1^凞.

Les courbes représentant les variations de ces grandeurs (prises souvent en valeurs relatives) en fonction de sont dites courbes de répartition spectrale de flux énergétique ou de flux lumineux, d’éclairement, etc. Les efficacités lumineuses K size=1^凞 et les facteurs de réflexion, de transmission ou d’absorption 福 size=1^凞, 精 size=1^凞 et 見 size=1^凞 monochromatiques sont de même relatifs à des lumières de longueur d’onde.

Récepteurs physiques

L’étude expérimentale des caractéristiques énergétiques d’un rayonnement se fait à l’aide de récepteurs physiques (cf. LUMIÈRE Optique). Les récepteurs thermiques (thermocouples, bolomètres, thermomètres pneumatiques très sensibles) ne sont pas sélectifs, c’est-à-dire que leur réponse, à énergie absorbée égale, ne dépend pas de la composition spectrale de la lumière. Ils permettent donc, en particulier, d’étudier directement la variation d’une grandeur énergétique monochromatique en fonction de la longueur d’onde, tout en établissant les courbes de sensibilité spectrale des récepteurs des autres types, qui sont tous sélectifs. Les récepteurs thermiques sont, d’autre part, seuls utilisables dans l’infrarouge lointain; mais, dans d’autres domaines du spectre, leur sensibilité est souvent inférieure à celle d’autres récepteurs physiques. Comme les récepteurs photoélectriques (cf. infra ), les récepteurs thermiques ont sur l’œil l’avantage d’offrir, par l’intermédiaire d’un courant électrique, des possibilités d’amplification, ainsi que d’enregistrement de phénomènes variant rapidement en fonction du temps.

La base de la photométrie photographique est la suivante: soit deux régions voisines d’un même cliché éclairées à des moments voisins, pendant un même temps t , par deux faisceaux de même composition spectrale, le cliché ayant subi, après cette exposition, un traitement uniforme de développement, de séchage et de fixage: de l’égalité ou de l’inégalité des noircissements, on peut déduire celle des éclairements E reçus.

La figure 14 donne, à titre d’exemple, le schéma d’un microphotomètre , ainsi appelé parce qu’il permet de déterminer les facteurs de transmission 精 de plages très petites du cliché P. On le nomme aussi densitomètre , car on traduit les résultats des mesures par les valeurs de la densité optique D = colg 精.

L’expérience montre que D varie en fonction de log E, comme l’indique la courbe 臨 de la figure 15. Une telle courbe étant construite d’après les valeurs D¹, D², D³... correspondant à des éclairements connus E¹, E², E³..., l’éclairement inconnu X se déduit de la valeur correspondante de D; la sensibilité maximale s’obtient lorsque le point de coordonnées X, D est sur la partie rectiligne, à pente maximale de 臨.

Si l’on doit comparer des éclairements très différents, on applique parfois la pseudo-loi de réciprocité, d’après laquelle le noircissement ne varie pas sensiblement quand le produit Et reste le même, mais les écarts à cette «loi» sont parfois importants.

La photométrie photographique se prête à l’appréciation des éclairements très faibles, dont elle permet d’accumuler les effets, ainsi qu’à l’enregistrement de lumières brèves qu’on peut étudier après coup à loisir. Elle fut, jusqu’à la découverte des cellules photoélectriques, la seule utilisable pour les lumières ultraviolettes auxquelles les autres récepteurs sont peu (ou pas) sensibles. Toutefois, elle est d’un emploi délicat, et, même dans les meilleures conditions, n’assure pas une précision meilleure que quelques pour-cent. On trouvera à l’article PHOTOGRAPHIE des indications complémentaires, concernant, notamment, la sensibilité spectrale des émulsions.

L’article LUMIÈRE, déjà cité, donne quelques indications sur les possibilités des récepteurs photoélectriques ; leur emploi en photométrie se répand de plus en plus. Aux cellules photoémissives à atmosphère gazeuse on préfère les cellules à vide, moins sensibles mais plus fidèles, et dont la réponse est proportionnelle à l’éclairement reçu. On amplifie au besoin le courant qu’elles débitent, ou bien on a recours à des cellules photomultiplicatrices .

Moins précises, mais d’emploi très simple puisqu’elles n’exigent pas qu’on leur associe une source de courant et qu’on peut les faire débiter dans des milliampèremètres relativement robustes, les photopiles , dites aussi cellules à couche d’arrêt , sont les éléments essentiels des posemètres photographiques.

Dans des cas exceptionnels, on a utilisé des piles photovoltaïques du type métal-électrolyte-métal, symétriques, débitant un courant quand on éclaire une de leurs électrodes.

Enfin, les variations de résistance de certains corps sous l’action de la lumière (photoconduction) se sont révélées assez stables pour permettre des mesures d’une précision acceptable; on les emploie surtout dans le proche infrarouge, jusqu’à 5 ou 6 猪m.

5. Observateur moyen. Photométrie physique

Certaines mesures photométriques particulièrement importantes et délicates consistent à déterminer les efficacités lumineuses K en fonction des longueurs d’onde correspondantes. On a:

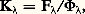si un faisceau monochromatique transporte un flux lumineux F size=1^凞d et un flux d’énergie 淋 size=1^凞 d. Cette efficacité a une valeur maximale K^m pour^m 黎 555 nm. Des mesures nombreuses et difficiles ont conduit à admettre: K^m 黎 680 lm/W.

Les lumières complexes ont une efficacité lumineuse très inférieure à K^m . Les sources de lumière monochromatique à efficacité élevée (vapeur de sodium) ne sont utilisables que si on ne cherche pas à percevoir les couleurs.

Plutôt que de mesurer directement l’efficacité K pour chaque longueur d’onde, on préfère parfois faire apparaître l’efficacité relative V size=1^凞, définie comme étant le rapport:

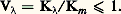Soit F^md et 淋^md les flux lumineux et énergétique transportés par un même faisceau de longueur d’onde^m . On a:

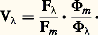La détermination de l’efficacité relative requiert ainsi seulement une comparaison des flux d’énergie, suivie d’une comparaison des flux lumineux.

Le tableau 3 indique les résultats déduits de nombreuses mesures caractérisant, par une convention adoptée en 1924, l’observateur normal moyen de la C.I.E. pour la vision diurne (ou photopique ).

La figure 16, représentant V size=1^凞, en fonction de, met en évidence la différence des résultats moyens obtenus par divers groupes d’observateurs. La dispersion des points entourant la courbe est due à des variations individuelles parfois considérables et à la difficulté des mesures, notamment dans la région des courtes longueurs d’onde. Il est probable que, dans un proche avenir, on modifiera certaines valeurs conventionnelles de V size=1^凞.

Quand l’œil est adapté à la vision nocturne (dite scotopique ), il perçoit moins bien les détails et les couleurs, mais mieux (par ses régions extrafovéales) les faibles luminances. Cette adaptation s’accompagne d’un accroissement relatif de sensibilité au bleu par rapport au rouge (phénomène de Purkinje) qui amène au voisinage de 510 nm la longueur d’onde du maximum d’efficacité (cf. COULEUR et VISION).

En admettant l’additivité des flux lumineux hétérochromes, on pourrait calculer le flux lumineux F d’un faisceau, dont on connaît la répartition spectrale du flux énergétique monochromatique 淋 size=1^凞, par la formule:

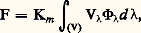l’intégrale, remplacée dans la pratique par une somme, étant étendue à tout le spectre visible (V).

Son efficacité lumineuse serait aussi calculable:

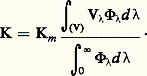Si l’on emploie ces formules, les opérations hétérochromes se réduisent à l’établissement de la fonction V de et, une fois qu’est choisi l’étalon de lumière, à la détermination de K^m . Toutefois, cela suppose des mesures énergétiques dont la précision est, dans la plupart des cas, encore insuffisante.

On a, à maintes reprises, proposé de réaliser des photomètres physiques donnant directement la valeur des flux lumineux F, par exemple. Ils pourraient comporter un récepteur thermique sur lequel F serait concentré, après que chacun de ses constituants monochromatiques aurait été réduit proportionnellement à la valeur correspondante de V size=1^凞. Cette réduction serait obtenue approximativement par l’interposition de filtres colorés, ou mieux, à l’aide d’un écran découpé de forme convenable, disposé dans un plan où l’on formerait un spectre réel de la lumière étudiée, qu’on recomposerait ensuite. Un récepteur photoélectrique serait aussi utilisable, sa sensibilité sélective spectrale nécessitant une modification du filtre. (C’est ce qu’on s’efforce de faire dans les luxmètres à photopile). Mais on n’a pas encore réalisé, sauf pour des usages très particuliers, un tel photomètre physique pouvant remplacer avantageusement les photomètres visuels.

6. Applications de la photométrie

Éclairage

Dans la plupart des cas, on utilise pour l’éclairage des sources lumineuses dont la couleur dite blanche rappelle celle de la lumière naturelle du soleil; mais pour certaines applications particulières (éclairage public, balisage de piste aérienne, lampes de laboratoire, etc.), on se sert de sources colorées.

L’éclairage électrique est, de loin, le plus fréquent, pour des raisons de commodité et d’économie. Les arcs au charbon ne se retrouvent que dans certains projecteurs et dans les phares.

Parmi les lampes couramment utilisées, on distingue essentiellement les lampes à incandescence, les lampes à décharge et les lampes fluorescentes. Aux lampes à incandescence à filament de carbone dans le vide ont succédé celles à filament de tungstène en atmosphère d’azote, d’argon ou de krypton, atmosphère qui limite la volatilisation du filament et permet d’améliorer la couleur, ainsi que le rendement, avec une luminance accrue; ces lampes fonctionnent à près de 3 000 K, avec une durée de vie de l’ordre de mille heures.

L’une des caractéristiques les plus importantes des lampes dites lampes à iode est la reconstitution quasi totale de leur filament en cours de fonctionnement. On introduit dans l’atmosphère inerte de la lampe une quantité de vapeur d’iode dosée avec précision. Cette vapeur capte le tungstène volatilisé pour former, au voisinage de la paroi (le plus souvent en quartz), de l’iodure de tungstène, WI², lequel, quand il parvient à proximité du filament, se décompose en libérant du tungstène qui se dépose à son endroit d’origine. Cette activité chimique particulière permet d’utiliser des températures encore plus élevées que dans les lampes classiques. L’usage des lampes à iode s’étend peu à peu à l’éclairage public, aux phares d’automobiles, et certains modèles sont prévus pour la photographie et le cinéma.

Le principe des lampes à décharge consiste à faire éclater et à entretenir dans un gaz convenablement choisi (vapeurs de sodium, de mercure, d’hydrogène, de xénon, etc.) une décharge électrique. Les lampes fluorescentes à basse tension sont constituées d’un tube en verre ayant une électrode à chacune de ses extrémités; à l’intérieur du tube règne une faible pression de vapeur de mercure, et la paroi est recouverte de substances fluorescentes. Après mise sous tension, un arc se forme entre les deux électrodes, créant un rayonnement ultraviolet intense, qui se transforme en radiations visibles par l’intermédiaire des poudres fluorescentes. Le montage électrique de ces lampes doit être réglé soigneusement pour éviter tout papillotement appréciable.

L’usager doit payer non pas la puissance rayonnée, mais la puissance consommée , compte tenu des pertes de chaleur dans les circuits électriques. Le rendement indiqué dans la colonne de droite du tableau 4 se rapporte à la puissance consommée; à côté du rendement, on doit considérer le coût de l’énergie utilisée, le prix d’achat du matériel et sa durée de vie.

Il faut éviter, dans le champ visuel, la présence de régions ayant une luminance ou une intensité trop élevée, qui entraîne une contraction pupillaire et des effets d’éblouissement bien connus des automobilistes roulant la nuit. La luminance maximale considérée comme tolérable est de l’ordre de 10⁶ nits.

En présence de sources ayant des luminances plus élevées, on utilise des diffuseurs ou des réflecteurs. Cela permet de mieux diriger la lumière, de la répartir sur les surfaces à éclairer, d’arrêter certains rayonnements dangereux tels que l’ultraviolet et de contribuer à la décoration des locaux ainsi qu’à la protection des lampes contre les intempéries.

L’éclairage est dit indirect quand la lumière est projetée vers une surface claire qui la réfléchit en la diffusant. Ce type d’éclairage atténue les ombres et réduit ainsi le relief des objets, la source étant complètement masquée, cela au prix d’une importante perte de lumière.

Les projets d’éclairage sont établis en évaluant le flux lumineux F nécessaire et sa répartition. On calcule F en multipliant les éclairements désirés par la surface des zones à éclairer, et en tenant compte des pertes par réflexion et transmission.

L’éclairement souhaitable varie selon qu’il s’agit de lieux de passage (vestibules, couloirs: 50 lux min.), ou de salles de lecture et de pièces où l’on exécute des «travaux fins» (300 lux min.).

Phares et projecteurs

Les phares destinés à être vus de loin, pour le repérage d’une direction ou d’un obstacle, et les projecteurs qui éclairent une route à suivre ou un objectif, ou encore un monument ou une scène de théâtre, utilisent une source de luminance L et de surface , placée au foyer d’un système optique réflecteur ou d’un réfracteur de surface S et de longueur focale f (fig. 17). Si le faisceau utile n’est pas trop ouvert, le flux lumineux reçu par cette optique est sensiblement F = L S/f ². L’ensemble des rayons issus de l’optique forme à peu près un tronc de cône d’angle solide 行 = /f ². L’éclairement produit à la distance x est sensiblement (aux pertes près):

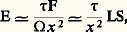精 étant le facteur de transmission de l’ensemble des pièces optiques et de l’atmosphère. Le phare se comporte donc, dans la région éclairée (aux pertes près, d’ailleurs importantes), comme une source d’intensité LS (ce produit est souvent appelé «puissance» du phare). Il y a intérêt à utiliser autant que possible des arcs de grande luminance et des optiques de grandes dimensions. On est limité, notamment, par la nécessité de former, à partir de chaque point de la source, un faisceau bien parallèle, ce qui interdit, S étant choisie, une valeur trop faible de f . Quant aux dimensions de la source, elles conditionnent, une fois f et S choisies, l’ouverture des faisceaux, qu’on se fixe selon l’utilisation prévue.

On trouvera dans les articles qui les concernent des indications sur les caractéristiques photométriques des instruments d’observation. Rappelons seulement que la luminance L de l’image (non ponctuelle) d’un objet de luminance L est:

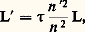n et n étant les indices de réfraction des milieux objet et image, et 精 le facteur de transmission des milieux interposés.

Le rapport des éclairements des images rétiniennes, qu’on appelle la clarté C est, par suite, sensiblement égal à 精 n ²/n ², tant que les diamètres de pupille oculaire dans la vision instrumentale (soit œ ) et dans la vision directe (soit œ ) sont égaux. Mais quand le grossissement G est assez grand, œ devient inférieur à œ , et C est réduite sensiblement dans le rapport: œ ²/œ ².

Dans l’observation des étoiles ou des particules ultramicroscopiques, en admettant que les flux F et F qui pénètrent dans l’œil, armé ou non de l’instrument, se concentrent sur les mêmes éléments rétiniens, on définit la clarté C comme le rapport F /F; on démontre que C varie avec G selon la loi: C = G²C.

Enfin, lorsqu’on forme des images réelles pour leur enregistrement photographique, on sait que leur éclairement varie à peu près en raison inverse du carré du «nombre d’ouverture» N = f /o , f étant la longueur focale de l’objectif, et o le diamètre de son diaphragme.

Dans tous les cas, la lumière parasite, résultant de réflexions sur la surface des verres et des montures, tend à voiler les images: elle doit être rendue aussi faible que possible, et ce sont encore des mesures photométriques qui permettent d’en juger.

Astronomie

La photométrie intervient en astronomie: on a mesuré la luminance du Soleil, de la Lune (tabl. 2), et même celle du ciel nocturne (de l’ordre de 10 size=1^漣8 nit, s’il n’y a pas de nuages). Mais cette notion ne peut s’appliquer aux étoiles que l’on voit comme des points. On les caractérise par leur éclat stellaire , qui est l’éclairement e que produit leur lumière, après traversée de l’atmosphère, sur un écran normal aux rayons.

Les étoiles étaient classées autrefois d’une façon empirique, celles qui nous paraissent le plus lumineuses étant dites de première grandeur, celles qui le sont un peu moins, de deuxième grandeur et ainsi de suite, la sixième grandeur correspondant à celles tout juste perceptibles par l’œil nu. Cette classification s’étant trouvée correspondre à une décroissance sensiblement logarithmique de l’éclat stellaire e , on est convenu d’appeler magnitude le nombre m = m ⁰ 漣 2,5 lg(e/e ⁰), e ⁰ étant l’éclat stellaire d’un astre de référence, de magnitude m ⁰ choisie de façon à raccorder au mieux la nouvelle échelle à l’ancienne ^{[cf. ASTRONOMIE ET ASTROPHYSIQUE]}. La notion précédente, appliquée à des astres autres que les étoiles, conduit à attribuer, par exemple, m 力 漣 4 à Vénus à son maximum de visibilité, 漣 12 à la pleine Lune, et 漣 27 au Soleil.

Spectrophotométrie

La spectrophotométrie permet d’évaluer, longueur d’onde par longueur d’onde, les grandeurs énergétiques ou photométriques «monochromatiques» définies précédemment. On isole les bandes spectrales choisies au moyen d’instruments convenables, dits monochromateurs ^{[cf. SPECTROPHOTOMÉTRIE]}, derrière lesquels on place un photomètre sensible visuel (sans écran diffusant), thermique ou photoélectrique, ou bien l’on compare les photographies des spectres des lumières étudiées.

Les résultats relatifs aux courbes spectrales de sensibilité des récepteurs ou de transmission des matériaux ont un intérêt pratique évident, et l’étude quantitative des spectres complète leur étude qualitative (détermination des longueurs d’onde) en ce qui concerne l’application des théories de l’émission et de l’absorption.

La colorimétrie, la polarimétrie, la photoélasticimétrie et la pyrométrie optique sont fondées, au moins pour une part, sur des mesures photométriques.

Enfin, l’action de la lumière sur la nature vivante n’a pu être étudiée et réglée au mieux que grâce à son évaluation au moins approximative. C’est ainsi qu’on a pu exprimer les doses érythémales de rayonnement ultraviolet à ne pas dépasser sous peine de coups de soleil ou de lésions plus ou moins graves, et celles qui sont nécessaires pour obtenir des effets antirachitiques, par un produit k Et , E étant l’éclairement énergétique, t la durée de son action, et k un facteur d’efficacité dépendant de la composition spectrale et de l’application envisagée. L’unité de dose, appelée finsen , correspond à une puissance de 10 microwatts agissant sur un être humain pendant une minute, si la longueur d’onde du rayonnement est de 297 nanomètres.

photométrie [ fɔtɔmetri ] n. f.

• v. 1729; de photo- et -métrie

♦ Anciennt Mesure des rayonnements lumineux par impression visuelle. — Métrol. Mesure des grandeurs relatives aux radiations électromagnétiques. Photométrie énergétique, visuelle. — Adj. PHOTOMÉTRIQUE , 1825 .

● photométrie nom féminin Mesure des grandeurs relatives aux rayonnements, évaluées selon l'impression visuelle produite par ceux-ci et sur la base de certaines conventions.

photométrie

n. f. PHYS Mesure de l'intensité d'une source lumineuse.

⇒PHOTOMÉTRIE, subst. fém.

A. —OPT. Étude et mesure de l'énergie transportée par le rayonnement électromagnétique, et plus particulièrement par la lumière visible (d'apr. SARM. Phys. 1978). Photométrie astronomique; photométrie photographique, photoélectrique. À la fin du XIX^e siècle, les courbes de lumière de plusieurs centaines d'étoiles avaient été déterminées, par photométrie visuelle directe en général (Hist. gén. sc., t.3, vol. 1, 1961, p.145). La photométrie du disque solaire dans différentes longueurs d'onde permet de mettre en évidence l'assombrissement au bord du disque, et son comportement pour les différentes longueurs d'onde (SCHATZMAN, Astrophys., 1963, p.43). Vers 1922, G. Rougier à (...) Strasbourg et Guthnick à (...) Babelsberg emploient les premières cellules photoélectriques au potassium pour la mesure des magnitudes stellaires et la photométrie de la lune (Hist. gén. sc., t.3, vol. 2, 1964, p.515).

B. —OPHTALMOL. Mesure de l'acuité visuelle (au moyen d'un photomètre) (d'apr. MAN.-MAN. Méd. 1977).

Prononc. et Orth.:[]. Att. ds Ac. 1935. Étymol. et Hist. 1758 opt. (J. H. LAMBERT, Les Propriétés remarquables de la route de la lumiere par les airs, 4-5 et passim ds QUEM. DDL t.26). Formé des élém. photo-¹ et -métrie prob. d'abord par un lat. sav. photometria (cf. LAMBERT, Photometria, 1760 Catal. Bibl. Nat.).

DÉR. Photométrique, adj. Qui a rapport, qui appartient à la photométrie. Expériences, procédés photométriques; analyse, loi photométrique. En ce qui concerne la lumière du jour, les données photométriques correspondent sensiblement à celles relatives à l'énergie calorifique (MAURAIN, Météor., 1950, p.238). Grâce au remplacement progressif de l'oeil humain par de nouveaux récepteurs, les mesures photométriques ont été étendues, avec une précision sans cesse accrue, à des astres de plus en plus faibles (Hist. gén. sc., t.3, vol. 2, 1964, p.550). — []. — 1^re attest. 1768 (LAMBERT, Mém. sur la partie photométrique de l'art du peintre, Hist. de l'Ac. royale des sc. et belles-lettres, t.24, Berlin, 1770); de photométrie, suff. -ique.

BBG. —QUEM. DDL t.10 (s.v. photométrique).

photométrie [fɔtɔmetʀi] n. f.

ÉTYM. 1812; de photo-, et -métrie.

❖

♦ Science.

1 Mesure des rayonnements par impression visuelle (photométrie visuelle).

2 Mesure de l'intensité des rayonnements visibles ou non visibles, quelle que soit leur place dans le spectre et quel que soit l'appareil de mesure employé. || Photométrie par égalisation de la brillance de deux plages lumineuses (et mesure de leur distance), par mesure du courant produit au moyen d'une cellule photo-électrique (luxmètres, posemètres), par la mesure du noircissement photographique (sensitométrie photographique).

❖

DÉR. Photométrique.

Encyclopédie Universelle. 2012.